Model summary
Here we provide a comprehensive summary of the model. In order to more easily visualize the model, it is recommended to run the python script in order to generate plots that show various aspects of the model.
Any model for realistic AGN jets must include black hole spin since jet powers depend steeply on spin, and because including spin provides a well-defined direction for the jets to be launched in. The spin (angular momentum) of BHs is best represented through the dimensionlesss spin parameter \(a=J_\mathrm{BH}c/M_\mathrm{BH}^2 G\), where \(J_\mathrm{BH}\) is its angular momentum. For theoretical reasons, its magnitude cannot grow above 1. It can be positive, representing prograde accretion, or negative, representing retrograde accretion.
Jet powers, in addition to depending on spin, also depend on which accretion state the black hole is in. We refer to these states by the shape of the accretion disk that surrounds the BH. We include three accretion states: the thick (or advection-dominated accretion flow; ADAF), thin (standard) and slim disk (super-Eddington accretion). Our main reference points for these disks are the following papers: Shakura & Sunyaev (1973), Narayan & Yi (1994) and Wang & Zhou. (1999), respectively.
The thick disk appears at low accretion rates, has very strong jets and is inefficient at spinning up the black hole. The thin disk, appearing at intermediate accretion rates, typically has weak jets, strong radiation and efficiently spins up the black hole. The slim disk, corresponding to super-Eddington accretion, has features of both: in terms of geometry, orbits and angular momentum, it is similar to the thick disk. It is optically thin, leading to strong radiation. However, it also has strong jets. We assume that each subgrid accretion disk launches jets and radiates at the same time, regardless of the type it is. However, we use expressions for the jet and radiative efficiencies that depend on the type of the disk, and which are physically motivated.
Transitions from one accretion state to another
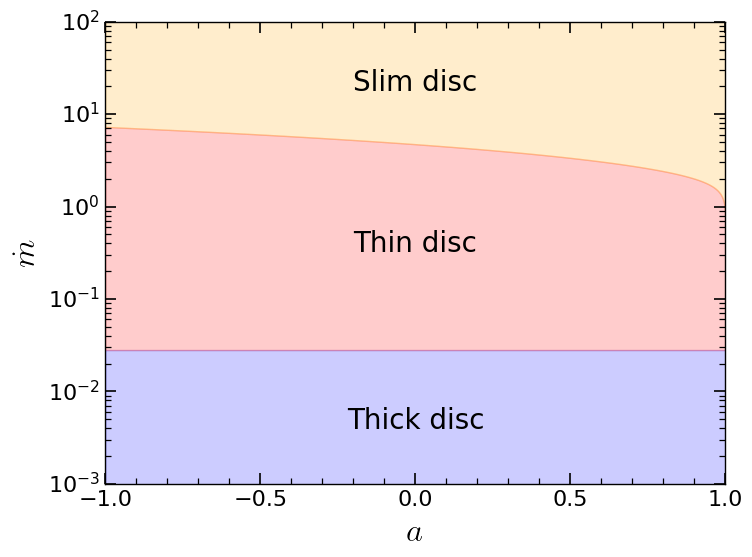
The type of accretion disk surrounding the BHs depending on their accretion rates and spins.
The state of the subgrid accretion disk depends mostly on the Eddington fraction, i.e. the (dimensionless) accretion rate of the BH in units of the Eddington accretion rate, which we denote as \(f_\mathrm{Edd}\). We assume that the subgrid accretion disk is thick for \(f_\mathrm{Edd}<f_\mathrm{Edd,crit,thick}\), where \(f_\mathrm{Edd,crit,thick}\approx0.01-0.03\) (based on observations; Russell et al. 2013) is a free parameter in the model. The accretion disc is assumed to be slim for \(f_\mathrm{Edd}>1\).
Accretion efficiencies
Our model requires the usage of accretion efficiencies, minimally in the thick disk regime. These accretion efficiencies arise due to winds that take away most of the accreting mass as it falls towards the BH. We supress the large-scale accretion rate (e.g. the Bondi rate), \(\dot{M}_\mathrm{BH,0}:\) such that the net accretion rate is equal to
where the terms in parenthesis are feedback efficiencies (discussed below), defined as \(\epsilon_i=P_i/\dot{M}_\mathrm{BH}c^2\), while \(\epsilon_\mathrm{acc}\) is the accretion efficiency.
In the thick and slim disk, we allow options where the accretion efficiencies are free parameters in the model, to be tuned somehow (in practice, for the thick disc efficiency, to the local AGN bolometric luminosity function). We also allow a more complex scaling for the thick disk, based on GRMHD simulations (e.g. Cho et al. 2024). These simulations show that the accretion efficiency in thick disks can be calculated as
where \(R_0\approx5-10\) (in units of \(R_\mathrm{G}\)), \(R_\mathrm{thick}\) is the radius of the hot accretion flow and \(s=0.5\) in recent such simulations. The radius \(R_\mathrm{thick}\) is the same as the Bondi radius if the accretion rate is very low. However, at high accretion rates (but still below \(f_\mathrm{Edd}\approx0.01\)), the accretion disk may be thin at large distances and thick at smaller ones, with the transition occuring at some radius \(R_\mathrm{tr}\). In this case, the winds (and mass loading) operate only at smaller radii. Given these considerations, we write
and we choose to parametrize \(R_\mathrm{tr}\) based on original calculations by Narayan & Yi (1995), who found the transition radius as the radius where half of the energy gets radiated away, and half advected inwards. Their formula can be written in the form
where \(R_1\) is some normalisation radius that depends strongly on the assumed value of the accretion disk viscosity parameter \(\alpha\). We instead leave \(R_1\) as a free parameter in our formulation. Note that at moderate Eddington ratios, where the Bondi radius is not the limiting radius (i.e. where a thin disk component exists outside the thick disk), we may write the accretion efficiency as:
where we have assumed \(s=0.5\).
Jet efficiencies
The jet efficiency is related to the jet power through \(\epsilon_\mathrm{j}=P_\mathrm{j}/\dot{M}_\mathrm{BH,0}c^2\), where \(\dot{M}_\mathrm{BH,0}\) is the accretion rate measured in the simulation, e.g. the Bondi rate). We use the formula for the jet efficiency based on general-relativistic, magneto-hydrodynamical (GRMHD) simulations by Tchekhovskoy et al. (2010):
where \(\kappa\approx0.05\) is a numerical factor which depends on the initial geometry of the magnetic field, \(\phi_\mathrm{BH}\) is the dimensionless magnetic flux threading the horizon (see original paper for precise definition), and \(\Omega_\mathrm{BH}=a/2r_\mathrm{H}\) is the (dimensionless) angular velocity of the black hole event horizon. Here, \(r_\mathrm{H}=1+\sqrt{1-a^2}\) is the radius of the horizon in units of the gravitational radius \(R_\mathrm{G}=M_\mathrm{BH}G/c^2\). The formula above, for the jet efficiency, agrees very well with the results from higher-resolution simulations performed by Narayan et al. (2021), who provide the following fit for the magnetic flux as a function of spin:
The Tchekhovskoy et al. (2010) jet efficiency depends very steeply on spin (\(\epsilon_\mathrm{j}\propto a^2\) for small spin and \(\epsilon_\mathrm{j}\propto a^6\) near \(a=1\)). It can reach values above 100 per cent for large spins, and is also different (weaker) for negative spins.
The dependence of the jet efficiency on the type of accretion disk is encoded in the fact that thick disks are thought to be in a magnetically-arred state (so-called MAD. see Narayan et al. 2003), while thin disks are likely not, because they do not feature strong advection. The slim disk, on the other hand, is thought to be similar to the thick disk in terms of advection, and thus probably in terms of jet powers. Recent simulations by Ricarte et al. (2023) have found an increase of \(\phi_\mathrm{BH}\) in the thin and slim disk regime as the Eddington ratio increases, and they parametrise this increase as
The magnetic flux eventually saturates (at very high \(f_\mathrm{Edd}\)) at the same value as that reached in the thick disc; \(\phi_\mathrm{BH,MAD}\).
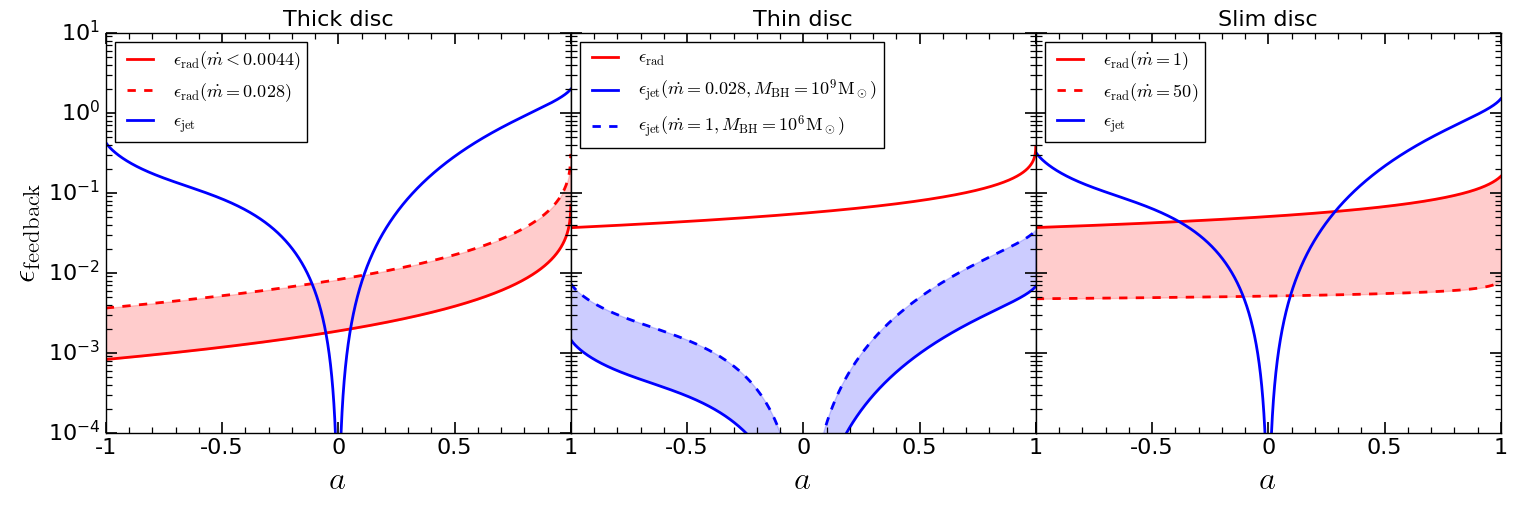
Feedback efficiencies (jet - blue, radiation - red) for all three accretion disk types. Shaded regions represent likely ranges of efficiencies (where the efficiencies depend on mass and/or accretion rate). The thin disk jet efficiencies were computed assuming the slope of the efficiency vs. aspect ratio relation is \(\eta=1\), and the aspect ratios were computed for region b) of the Shakura & Sunyaev solution. Radiative efficiencies in the thick disk were computed assuming the electron heating parameter \(\delta=0.2\).
Radiative/wind efficiencies
In the EAGLE and COLIBRE models, all subgrid accretion disks are effectively thin, and the BH is always assumed to be in this regime. In our model, the radiative efficiency (defined in an analagous way to the jet efficiency, but using the luminosity) is no longer fixed at a value of order \(10\) per cent. Instead, we use spin-dependant formulas that vary with the type of disk. In the thin disk, the radiative efficiency \(\epsilon_\mathrm{r,TD}\) is related to the binding energy at the innermost stable circular orbit (ISCO) and is given by
Here, \(r_\mathrm{ISCO}\) is the radius of the ISCO in gravitational radii (see e.g. appendix B of Fiacconi et al. 2018 for an expression giving the spin dependence). The radiative efficiency of the thin disk grows slowly from its minimum value of \(\approx4\) per cent for \(a=-1\) to \(\approx5.5\) per cent for \(a=0\). For positive spins it grows more steeply; it is \(10\) per cent by \(a=0.65\). Beyond that the dependence steepens even further, with values of \(20\), \(30\) and \(40\) per cent reached at \(a=0.95\), \(a=0.997\) and \(a=1\), respectively.
In the thick disk regime, radiative efficiencies are lower by a factor \(\approx100\) than jet efficiencies. The formulas we use are based on results by Mahadevan (1997), who studied cooling processes of electrons (which dominate in the radiation) in the context of the original thick disc solution. They found two different regimes: for \(f_\mathrm{Edd}<f_\mathrm{Edd,crit,visc}\), viscous heating dominates the heating of electrons, whereas for \(f_\mathrm{Edd,crit,visc}<f_\mathrm{Edd}<f_\mathrm{Edd,crit,ADAF}\), it is dominated by ion-electron heating. Here, \(f_\mathrm{Edd,crit,visc}\) is the transitional value between the two thick disc (ADAF) regimes, and \(f_\mathrm{Edd,crit,ADAF}=0.4\alpha^2\) is the transitional accretion rate which separates thin and thick discs. The radiative efficiency in the viscous heating regime is given by
while in the ion-heating regime it is given by
Here, \(\beta\) is the ratio of gas pressure and total pressure (which includes the magnetic pressure). Yuan & Narayan (2014) define a somewhat different parameter, \(\beta_\mathrm{ADAF}\), as the ratio of gas pressure and magnetic pressure. The two parameters are related by \(\beta=\beta_\mathrm{ADAF}/(1+\beta_\mathrm{ADAF})\). \(\beta_\mathrm{ADAF}\) is not an independent parameter; many simulations have found that \(\alpha\beta_\mathrm{ADAF}\approx0.5\) (e.g. Begelman et al. 2021, see also Yuan & Narayan 2014 for a review), which we adopt. \(\delta_\mathrm{ADAF}\) represents the fraction of viscous energy transferred to the electrons, and is constrained in theoretical studies between 0.1 and 0.5 (Yuan & Narayan 2014, Sharma et al. 2007). Observations imply a value close to 0.2 (Yuan et al. 2003, Liu & Wu 2013). The critical accretion rate between the two thick disc regimes can be found by ensuring that both formulas presented above yield the same radiative efficiency (at that accretion rate). This gives an accretion rate equal to
For slim disks we take the radiative efficiency based on GRMHD simulations of super-Eddington accretion (for various BH spins) performed by Sadowski et al. (2014). Madau et al. (2014) found the following fitting function which represents the Sadowski et al. (2014) results:
where the three spin-dependant functions are given by \(A(a)=(0.9663-0.9292a)^{-0.5639}\), \(B(a)=(4.627-4.445a)^{-0.5524}\) and \(C(a)=(827.3-718.1a)^{-0.7060}\). The radiative efficiency of slim disks, based on this formula, matches the thin disk radiative efficiency (given at the beginning of the section) at low accretion rates. At high accretion rates (\(f_\mathrm{Edd}\gtrapprox1\), but depending on spin), the radiative efficiency drops.
The thin disc radiative efficiency is used to source feedback in the simulations. In the thin disk regime, a fraction \(\epsilon_\mathrm{f}\approx0.1\) of all of the radiation released by black holes couples to the gas in the form of thermal energy. In the thick and slim disk, we do not use radiation to source feedback. We do, however, assume that winds launched from the accretion disk are present in these two states. In the thick disk, winds are thought to be launched on account of a combination of gas pressure and MHD effects. We use the formula from Sadowski et al. (2013):
For the slim disk, we again use results from Ricarte et al. (2023), as we did for the jet efficiency. We use their total MHD efficiency and subtract from that the analytical jet efficiency as given by the formula we use as a function of spin and magnetic flux. We then found a simple fitting function to the remaining efficiency, representing the wind:
Evolution of the black hole spin magnitude
The BH spin (or angular momentum) is, naturally, a vector. However, due to Lense-thirring torques (we discuss these in more detail below), the accretion disk is always either aligned or counteraligned with the rotational axis of the black hole. This means that almost all relevant quantities, such as the efficiencies discussed above, can be expressed as depending only on the magnitude of spin, but also allowing for a negative sign to account for counteraligned disks (retrograde accretion). This is also true for the evolution of the magnitude of spin.
In the absence of jet spindown, the evolution of angular momentum is given simply by \(\dot{J}_\mathrm{BH}=L_\mathrm{in}\dot{M}_\mathrm{BH}\), where \(L_\mathrm{in}\) is the specific angular momentum at the inner radius of the accretion disk. This can be transformed into an equation for spin evolution, yielding
where \(\ell_\mathrm{in}\) is the specific angular momentum in units where \(G\) and \(c\) are equal to unity, and \(\mathrm{d}\ln M_\mathrm{BH,0}=\mathrm{d}M_\mathrm{BH,0}/M_\mathrm{BH}\) is the logarithmic change in mass, not including losses due to radiation (Fanidakis et al. 2011). The specific binding energy can be related to the radiative efficiency through \(e_\mathrm{in}=1-\epsilon_\mathrm{r}\) for all three accretion states (for the thick disc, the radiative efficiency is negligible for this application). All of the above quantities are evaluated at some inner radius beyond which gas orbits are unstable.
To be consistent with what we assumed for feedback efficiencies, we take results for the spinup/spindown function directly from GRMHD simulations. For the thick disc, we use the formula from Narayan et al. (2021):
For the slim and thin disc, we use results from Ricarte et al. (2023), who find a fitting formula that smoothly interpolates between the thin disc regime without significant jet feedback (for \(f_\mathrm{Edd}\) not close to super-Eddington values), and that where jet feedback essentially matches the thick disc (and so jet spindown should also be similar). Their formula takes the form
where the first term is a pure hydrodynamical term, while the second is an electromagnetic term. The first term is given by
where \(\xi=0.017f_\mathrm{Edd}\), \(s_\mathrm{min}=0.86-1.94a\) and \(s_\mathrm{thin}=\ell_\mathrm{ISCO}-2a e_\mathrm{ISCO}\) is the spinup/spindown function of the ‘pure’ thin disc (with no outflows and outside the MAD regime), in which \(\ell_\mathrm{ISCO}\) and \(e_\mathrm{ISCO}\) are the (dimensionless) specific angular momentum and binding energy, respectively, at the ISCO. The EM term is given by
where \(\epsilon_\mathrm{EM}\) is the total (jet+wind) EM efficiency, and \(k\) is given by
for positive spins \(a>0\) and by \(k=0.23\) for negative spins \(a<0\).

Spinup/spindown function (the dimensionless rate of black hole spin evolution) as a function of spin for all three accretion disk types. For the thin and slim disk, we show several curves for different choices of the Eddington ratio.
Evolution of the black hole spin direction
In the previous section we claimed that the evolution of the magnitude of spin depends only on whether accretion is prograde or retrograde. The two remaining questions are: 1) what about its direction, and 2) how to decide whether accretion is prograde or retrograde. We will now address the first of these.
Lense-Thirring torques (Lense & Thirring 1918) arise from additional GR forces that operate near spinning BHs, related to the frame-dragging of spacetime. In isolation, they cause the precession of a parcel of gas as it orbits around the BH. For accretion disks, their effects depend on the type of disk (see Nixon & King 2016 for a review). Lense-Thirring torques do not have a component in the direction of the BH spin vector, which is why they do not play a role in the evolution of the magnitude of spin.
In all cases, Lense-Thirring torques are effective only within some radius \(R_\mathrm{warp}\), which marks the boundary between the outer disk and an inner region, within which the BH can ‘communicate’ through these torques with the disk. Within this radius, the disk is on average aligned or counteraligned with the BH, whereas outside it, it is aligned with some large-scale angular momentum direction (which we can measure in the simulation) - hence the name warp radius. Given some surface density, one can also define the warp mass \(M_\mathrm{warp}\) and the warp angular momentum \(J_\mathrm{warp}\) as the total mass and angular momentum within \(R_\mathrm{warp}\), respectively. We will discuss how all of these warp-related quantities are calculated in each of the accretion disks further below, but for now we focus on how these warped disks feature in our model.
In terms of the evolution of the spin direction, the main assumption of our model is as follows (see King et al. 2005 for the original argument, and additional discussions in e.g. Fanidakis et al. 2011, Fiacconi et al. 2018 and Griffin et al. 2019a). All matter that flows through an accretion disk is aligned or counteraligned with the BH spin vector in the accretion process. Due to conservation of angular momentum, the spin vector itself also has to adjust to keep the total angular momentum conserved. In the process of consuming one warp mass \(M_\mathrm{warp}\), the direction of the BH spin vector is aligned to match the direction of the total angular momentum of the system comprising the BH and the disk out to the warp radius. The direction of the BH spin vector can then be determined from \(\vec{J}_\mathrm{warp}=\vec{J}_\mathrm{BH}+J_\mathrm{warp}\hat{J}_\mathrm{d}\), where \(\vec{J}_\mathrm{BH}\) is the old BH angular momentum vector, and \(\hat{J}_\mathrm{d}\) is the direction of the large-scale accretion disk (which we assume matches the direction of the angular momentum of the gas in the BH smoothing kernel).
In practice, the BH will consume parcels of mass that differ from \(M_\mathrm{warp}\). We assume that any such parcel of mass \(\Delta M\) (e.g. the mass to be consumed within a single time step) can be split up onto \(n=\Delta M / M_\mathrm{warp}\) individual increments of accretion, so the total angular momentum of the system within that time step is \(\vec{J}_\mathrm{warp}=\vec{J}_\mathrm{BH}+n J_\mathrm{warp}\hat{J}_\mathrm{d}\), i.e. \(n\) warp angular momenta are consumed, with an angular momentum of \(\Delta \vec{J}=n J_\mathrm{warp}\hat{J}_\mathrm{d}=(J_\mathrm{warp}/M_\mathrm{warp})\Delta M\). This can also be viewed as the BH consuming material with a specific angular momentum of \(L_\mathrm{warp}=J_\mathrm{warp}/M_\mathrm{warp}\). Note that this picture is only valid if the BH spin vector does not change much during this process (in both magnitude and direction), which can be ensured with wisely chosen time steps.
Deciding whether accretion is prograde or retrograde
We now discuss how to decide whether the sign of spin is positive or negative. In the process of communicating with the inner disk through Lense-Thirring torques, the disk either aligns or counteraligns with the BH spin vector. The condition for which of the two occurs can be derived by assuming that the magnitude of the spin does not change during this alignment (King et al. 2005). Accretion is retrograde if
where \(\cos \theta=\hat{J}_\mathrm{BH}\cdot\hat{J}_\mathrm{d}\) is the angle between the initial spin vector and the large-scale angular momentum of the disk. If this condition is not fulfilled, accretion is assumed to be prograde. Note that retrograde accretion is only possible if the angle between the spin vector and the large-scale accretion disk is larger than \(90^\circ\), and if the warp angular momentum is comparable to the BH one.
Structure of the warped and precessing accretion disk
As mentioned already, Lense-Thirring torques have different effects depending on the type of accretion disk. In particular, their effects depend on the ratio of the viscosity parameter \(\alpha\) and the aspect ratio \(H/R\). For thin discs (\(\alpha\gg H/R\)), the disk is exactly warped as in the manner described in the preceeding two sections (Bardeen & Peterson 1975). The radius \(R_\mathrm{warp}\) which separates the inner and outer accretion disc can be calculated by equating the Lense-Thirring precession time-scale (\(t_\mathrm{p}=2\pi/\Omega_\mathrm{p}\), with \(\Omega_\mathrm{p}=2GJ_\mathrm{BH}/c^2R^3\) the precession rate) and the vertical warp propagation time-scale (\(t_\mathrm{warp}=R^2/\nu_2\), with \(\nu_2\) the kinematic viscosity in the vertical direction) (e.g. Martin et al. 2007). The vertical kinematic viscosity \(\nu_2\) can be related to the horizontal one, \(\nu_1\), by \(\nu_2=\xi\nu_1\), with \(\xi\) a numerical parameter given by
(Ogilvie 1999, see also Lodato et al. 2010 for a detailed discussion). We use the relation \(\dot{M}=3\pi\nu_1 \Sigma\) to calculate \(\nu_1\), and therefore \(\nu_2\). The warp radius will depend on which region of the thin disc we assume, with each having its own expression for \(\Sigma\). In region b) of the Shakura & Sunyaev (1973) thin disk, the surface density can be expressed as
while in region c) we have
These relations lead to the following expressions for \(R_\mathrm{warp}\):
(in region b) and
(in region c), with \(R_\mathrm{S}=2R_\mathrm{G}\) the Schwarzschild radius. These warp radii are generally of order \(\approx1000R_\mathrm{G}\), which can lead to fairly quick alignment of the thin disk with the large-scale angular momentum direction (quicker than any significant evolution in mass or spin magnitude, illustrating why the inclusion of the effects of Lense-Thirring torques is important).
In the context of thin disks, there is a futher complication. The self-gravity of the disk may become important at large radii (see Lodato 2007 for a review). The disk will fragment in the region where the Toomre parameter is \(Q(R)>1\). We thus assume that the disk extends out to where \(Q(R_\mathrm{sg})=1\). The self-gravity radius \(R_\mathrm{sg}\) can be calculated from this condition and the definition of the Toomre parameter \(Q=\Omega c_{\mathrm{s}} /(\pi G \Sigma)\), yielding
in region b) and
in region c). In all our calculations involving \(R_\mathrm{warp}\) (for deciding the sign of spin and evolving the direction of angular momentum, as described in the preceeding sections), we always take the minimum of \(R_\mathrm{warp}\) and \(R_\mathrm{sg}\). This is because if \(R_\mathrm{sg}<R_\mathrm{warp}\), the entire disk of extent \(R_\mathrm{sg}\) will be warped.
The thick disk does not experience the Bardeen-Peterson effect, i.e. it is never truly aligned nor counter-aligned in its inner regions. Instead, the disk precesses out to several dozen \(R_\mathrm{G}\), as seen in simulations (e.g. Fragile et al. 2007), and likely observations through quasi-periodic oscillations (QPO; e.g. Ingram et al. 2012). The slim disk has received much less attention in both simulations and observations (it is both harder to simulate and observe), but its similarity to the thick disk in its geometric aspects likely means that it precesses in a similar manner.
The exact behaviour of the thick and slim disk (which we will collectively call the advection-dominated disks) again depends on the ratio of \(\alpha\) and \(H/R\). Unfortunately, the advection-dominated disks both satisfy \(\alpha\approx H/R\), and in this regime, the effects of Lense-Thirring torques are not well understood from a theoretical perspective. However, if \(\alpha\ll H/R\) (the so-called bending-wave regime), Lense-Thirring torques are known to cause precession of the entire inner disk as a solid body, as seen in observations and simulations. For simplicity, we will thus assume this to be the case for advection-dominated disks.
Lubow et al. (2002) studied the bending-wave regime. In the inner regions, the disk precesses around the spin axis, while in the outer regions, it is aligned with the large-scale angular momentum of the disk. Based on their results the transition radius between the precessing and non-precessing regions of the disk given by
In our model, we assume that the inner regions of the disks are on average aligned or counteraligned with the spin vector (one can think of this as averaging over the precession, which has periods of \(\approx\) days, over long enough time scales). For simplicity, we also refer to the radii within which this is true as the warp radii. For both of the advection-dominated disks, these radii are only of order several \(R_\mathrm{G}\). Note that similar values are found if one assumes that the Bardeen-Peterson effect operates in these disks. While there are some uncertainties in the assumptions we have made, we point out that using any of these values is much more physically motivated than using thin disk equations (the warp radii of order thousands of \(R_\mathrm{G}\)), which is what is often done (e.g. Griffin et al. 2019a, Dubois et al. 2012).
In order to determine the sign of spin and evolve the angular momentum direction, expressions for the warp mass \(M_\mathrm{warp}\) and warp angular momentum \(J_\mathrm{warp}\) are also needed. We calculate this using surface integrals as
and
respectively. Here, \(L(R)\) is the specific angular momentum. In the case of the thin disk, we assume Keplerian orbits, i.e. \(L(R)=\sqrt{M_\mathrm{BH}G R}\). For the advection-dominated disks, we assume that they are smaller by a numerical factor \(\Omega_0\), which is given in the self-similar solutions for the thick (Narayan & Yi 1995b) and slim disk (Wang & Zhou 1999), seperately. The surface densities in both of these accretion disks are given by the same formula in the self-similar solutions, which is
where \(v_\mathrm{r}=-\alpha v_0 v_\mathrm{K}\) is the radial velocity. Here, \(v_\mathrm{K}=\sqrt{M_\mathrm{BH}G/R}\) is the Keplerian velocity, and \(v_0\) is another numerical coefficient that differs between the two solutions. In the thick disk, the numerical coefficients are given by \(v_0=3/(5+2\varepsilon)\) and \(\Omega_0=\sqrt{2\varepsilon/(5+2\varepsilon)}\), where \(\varepsilon=(5/3-\gamma)/(\gamma-1)\). The adiabatic index depends on how magnetized the disk is. In particular, it depends on the gas-to-total pressure ratio as \(\gamma = (8-3\beta)/(6-3\beta)\), and \(\beta\) itself depends on \(\alpha\) (see discussion above on radiative efficiency in the thin disk). \(v_0\) varies weakly with \(\alpha\); for \(\alpha=0.05\), it is \(0.56\), whereas for \(\alpha=0.3\), it evaluates to 0.5. \(\Omega_0\) depends on \(\alpha\) somewhat more strongly; we obtain \(0.27\) and \(0.41\) for the same values of \(\alpha\). The latter value agrees well with the ratio of actual to Keplerian (ISCO) orbital velocity at the event horizon, which is \(0.45\). For the slim disc, \(v_0=\Omega_0=1/\sqrt{\gamma}\), with \(\gamma=5\).
Black hole mergers
In the process of merging, BHs interact in a very complicated manner. Their final spin is not trivial to predict, and it can depend on a very large parameter space (including the mass ratio of the black holes and the relative orientation and magnitude of the spins). Orbital angular momentum plays a role in the merger as well. We use the fitting function found by Rezzolla et al. (2009), whose results have been found to be very accurate in newer and more sophisticated studies that sweep the huge parameter space of possible merger configurations. These formulas are also applicable to cosmological simulations, since they cover the scenario of inspiral from very large distances.
The final spin, according to Rezzolla et al. (2009) can be calculated as
where \(q=M_2/M_1\) is the mass ratio (such that \(M_2<M_1\)), \(\mathbf{a}_1\) and \(\mathbf{a}_2\) are the spin vectors, and \(\mathbf{l}\) is a vector whose direction is the same as that of the orbital angular momentum \(\mathbf{L}\) (in the centre-of-mass frame), while its magnitude is given by
Here, \(\mu=q/(1+q)^2\) is the symmetric mass ratio, and \(s_4 = -0.1229\), \(s_5 = -0.4537\), \(t_0 = -2.8904\), \(t_2 = -3.5171\), \(t_3 = 2.5763\). The three cosines depend on the angles between the different vectors which play a role in the merger: \(\cos \phi=\hat{\mathbf{a}_{1}} \cdot \hat{\mathbf{a}_{\mathbf{2}}}\), \(\cos \theta=\hat{\mathbf{a}_{1}} \cdot \hat{\mathbf{l}}\), \(\cos \xi=\hat{\mathbf{a}_{2}} \cdot \hat{\mathbf{l}}\).
Given the information available within the model, we could in principle calculate the recoil velocity of the remnant, as well as the total mass fraction lost to gravitational waves. We do not implement the former at this stage since we cannot reliably track the movement of black holes in their host galaxies. However, we do implement the latter. We use results from the same series of numerical relativity simulations as above (Barausse et al. 2012) and write the final mass of the remnant as:
where \(p_0=0.04827\), \(p_1=0.01707\) and \(e_\mathrm{ISCO}(\tilde{a})\) is the dimensionless specific binding energy at the innermost stable circular orbit calculated using an effective spin variable defined as